Statistical Skier

My post on the differing performance of Japanese skiers by technique (classic vs. freestyle) got a lot of positive responses and a few requests that I use the same methods on some other countries.  First up is Italy.

I’ve tweaked and refined my model a fair bit, hopefully for the better.  The basic idea is the same: using a hierarchical linear model to estimate differences in performance in skating and classic races (I’m omitting pursuits of all varieties).  There are some technical things I’ve changed to be able to accomodate changes over time.  Mostly this means making some adjustments for the occasional small sample sizes you find from season to season.  This allows me to provide an estimate even in seasons where a skier did races of only one technique, although naturally those estimates come with a bit of a grain of salt.

In the results by athlete for their entire career, I’m only going to display information on only those athletes that did a minimum number of races of each technique (2) for space and clarity reasons.

The final big change is in the distance category.  There are some technical reasons why FIS points are somewhat of a nuisance to use as a response variable in models like these, so I’m using something else: percent back from the median skier.  I’ll save a more detailed description for why I’m doing this and how this measure is useful for another post.  Here all we need to know is that 0% back represents the median (or middle) WC skier.  Negative values mean you’re faster and positive values mean you’re slower.

Going into this, our intuitive notion is that the Italians have been generally better at skating.  And that does turn out to be the case.  But some other fascinating stuff pops up as well.

Distance

Here are the estimates for the effect on median percent back of freestyle races for each Italian skier, over their entire career:

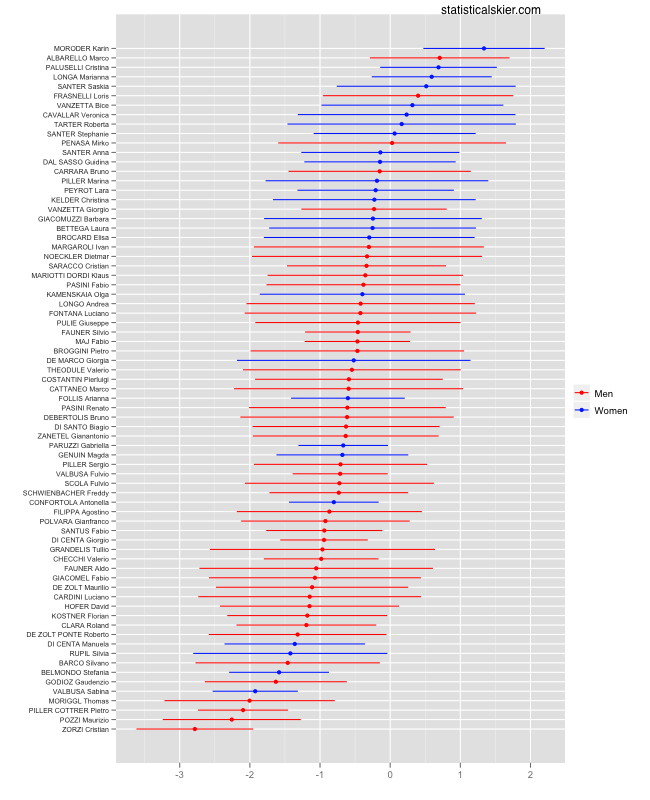Remember that the x axis is the change in median percent back for freestyle races.  So negative values here mean that that athlete was better in freestyle.

Clearly, with the overwhelming majority of skiers falling in the negative range, often times statistically significantly so, we’re seeing a strong preference for skating.  But do you notice a difference in the color pattern?  This preference for skating seems much less strong among the Italian women.  Sure, there are several well known Italian women who were significantly better at skating (Belmonda, Di Centa, etc.) but you’ve got this mass of blue up at the top.

Not many actually have better performance in classic skiing, but the difference between the two seems much less than with the men.

Now let’s look at how this has changed over time across the entire team:

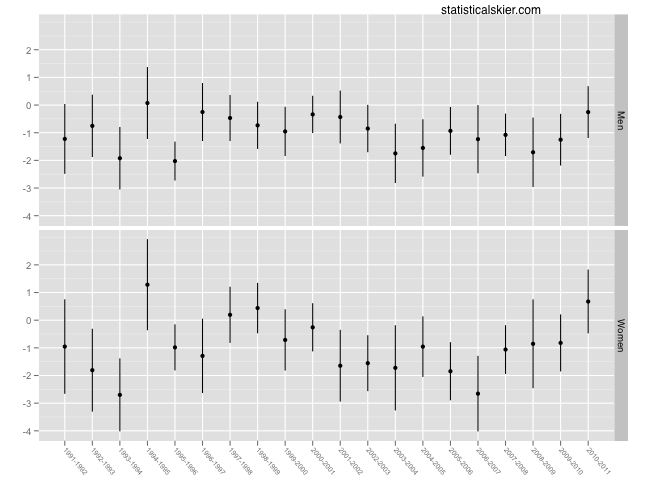Once again, negative values (this time on the y axis) represent the team as a whole performing better at skate races.  Note that I’ve included estimates for the 2010-2011 season, but we shouldn’t put much weight on those since the season is only just begun.

Both the women and the men have bounced around mostly below zero (better at skating) and oftentimes significantly so.  There might be a slight increase in this trend for the men (discounting the estimate for 2010-2011), but it is very small.  The women have a clearer trend, showing an increased discrepancy towards skating through much of the 2000’s but seem to have reversed that somewhat over the last 3 years or so.

Something looks extremely unusual in the earlier season, particularly with 1994-1995.  Normally when doing data analysis I’d go back and dig deeper into the model to see what’s going on there, but I have time for only so much investigation.  The question to keep in mind is whether the effect in that season is “real” or is it an artifact of my model?  In either case, I have less confidence that my model is working for the early 90’s.

Sprint

The results for the sprinters is more straightforward to interpret, since I’m just using rank as a measure.  First up the individual athletes:

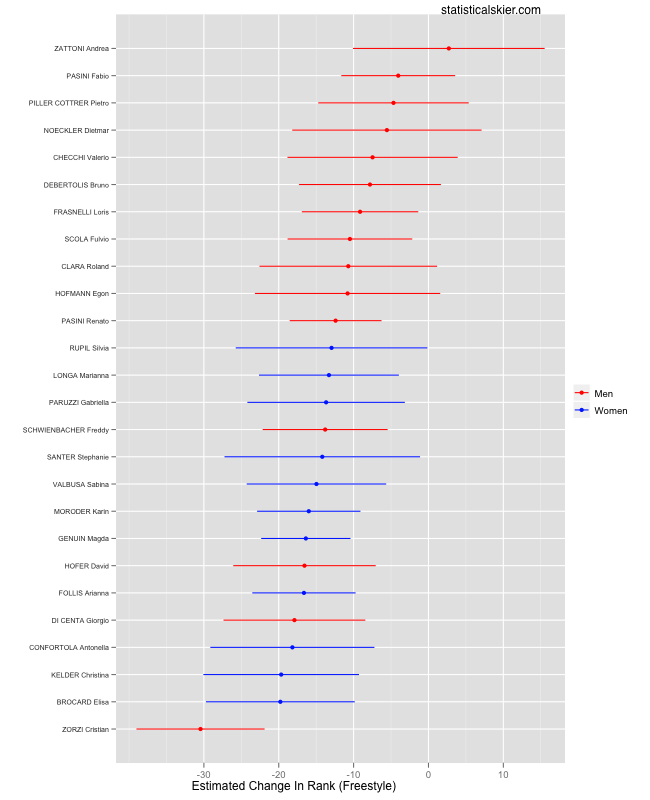Once again a clear, strong tendency towards skating (a negative change in rank means you did better in skate sprints).  And the gender difference is even stronger here, but it’s reversed! Here, while both men and women generally do better in skate sprints, this difference is considerably larger for the women.

How have these differences changed over time?

Sprinting hasn’t been around as long and I’m chopping off some of the early, experimental years of the event.  Again, don’t put much faith in the estimate for 2010-2011; it will surely change!

Both the men and the women seem fairly stable, actually.  The men were more tilted toward skating prior to 2006-2007, and the women may perhaps have seen a slight easing of their preference for skating as well.  But you really have to squint.

My final point here is to observe the difference in the confidence intervals at the individual level versus the team level.  Nearly all of the effects at the individual level appear statistically significant (the error bars don’t overlap zero), but at the team level this doesn’t seem to be the case, even though the preference for skating is still apparent.  This is one of the reasons why hierarchical models are so useful; you can separate out these sorts of effects at different levels.

Next up…..Norway!

[ad#AdSenseBanner]